一、1到10的立方根和1到30的平方根是多少？

1到10的立方根：

1的立方是1；

2的立方是8；

3的立方是27；

4的立方是64；

5的立方是125；

6的立方是216；

7的立方是343；

8的立方是512；

9的立方是729；

10的立方是1000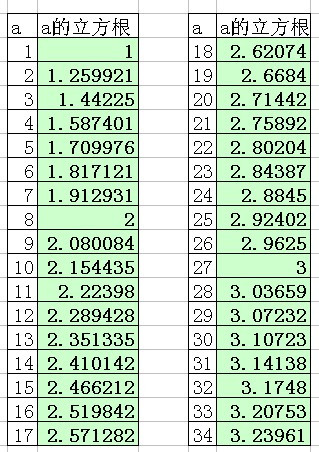

1到30的平方根：

1的平方是1；

2的平方是4；

3的平方是9；

4的平方是16；

5的平方是25；

6的平方是36；

7的平方是49；

8的平方是64；

9的平方是81；

10的平方是100；

11的平方是121；

12的平方是144；

13的平方是169；

14的平方是196；

15的平方是225；

16的平方是256；

17的平方是289；

18的平方是324；

19的平方是361；

20的平方是400；

21的平方是441；

22的平方是484；

23的平方是529；

24的平方是576；

25的平方是625；

26的平方是676；

27的平方是729；

28的平方是784；

29的平方是841；

30的平方是900。

牛顿迭代法：

笔算开方方法是我们大多数人上学时课本附录给出的方法，实际中运算中太麻烦了。我们可以采取下面办法：

比如136161这个数字，首先我们找到一个和136161的平方根比较接近的数，任选一个，比方说300到400间的任何一个数，这里选350，作为代表。

我们先计算0.5(350+136161/350)，结果为369.5。

然后我们再计算0.5(369.5+136161/369.5)得到369.0003，我们发现369.5和369.0003相差无几，并且369²末尾数字为1。我们有理由断定369²=136161。

一般来说，能够开方开的尽的，用上述方法算一两次基本结果就出来了。对于那些开方开不尽的数，用这种方法算两三次精度就很可观了，一般达到小数点后好几位。实际中这种算法也是计算机用于开方的算法。

二、1到10的立方根

±1：±1.00000，±2：±1.25992，±3：±1.44225，±4：±1.58740

±5：±1.70998，±6：±1.81712，±7：±1.91293，±8：±2.00000

±9：±2.08008，±10：±2.15443。

扩展资料：

平方根与立方根的联系与区别如下。

区别

（1）定义不同

平方根：如果一个数的平方等于 a，那么这个数就叫 a 的平方根或二次方根．即如果  ，那么 x 就叫 a 的平方根；立方根：如果一个数的立方等于 a，那么这个数叫做 a 的立方根或三次方根．即如果  ，那么 x 叫做 a 的立方根。

（2）表示方法不同

平方根用“  ”表示，根指数 2 可以省略；算术平方根用“  ”表示，根指数 2 可以省略；立方根用“  ”表示，根指数 3 不能略去，更不能写成“  ”

（3）存在的条件不同

a 有平方根的条件：  ，因为正数、零、负数的平方都不是负数，故负数没有平方根和算术平方根。a 有立方根的条件：a 为全体实数，即正数、负数、零均可。

参考资料：百度百科-立方根

三、1的立方根是多少？

1的立方根是1，1X1=11÷1=1。

（1）在实数范围内，任何实数的立方根只有一个。

（2）在实数范围内，负数不能开平方，但可以开立方。

（3）0的立方根是0。

扩展资料

平方根与立方根的联系：

平方根：如果一个数的平方等于a，那么这个数就叫a的平方根或二次方根．即如果，那么x就叫a平方根；立方根：如果一个数的立方等于a，那么这个数叫做a的立方根或三次方根．即如果，那么x叫做a的立方根。

四、1~20立方根表

立方根 ：

3√0 = 0 。

3√1 = 1 。

3√2 = 1.25992104989487 。

3√3 = 1.44224957030741 。

3√4 = 1.5874010519682 。

3√6 = 1.81712059283214 。

3√7 = 1.91293118277239 。

3√8 = 2 。

3√9 = 2.0800838230519 。

3√10 = 2.15443469003188 。

3√11 = 2.22398009056932 。

3√12 = 2.28942848510666 。

3√13 = 2.35133468772076 。

3√14 = 2.41014226417523 。

3√15 = 2.46621207433047 。

3√16 = 2.51984209978975 。

3√17 = 2.57128159065824 。

3√18 = 2.6207413942089 。

3√19 = 2.66840164872194 。

3√20 = 2.71441761659491 。

3√21 = 2.75892417638112 。

3√22 = 2.80203933065539 。

3√23 = 2.84386697985157 。

3√24 = 2.88449914061482 。

3√25 = 2.92401773821287 。

3√26 = 2.96249606840737 。

3√27 = 3。

概念

一般地，如果一个数X的立方等于 a，那么这个数X就叫做a的立方根(cube root，也叫做三次方根)。也就是说，如果x3=a，那么x叫做a的立方根。

读作"三次根号a"。其中，a叫做被开方数，3叫做根指数(a可以等于所有数，包括0)。如果被开方数还有指数，那么这个指数(必须是能被3整除的)还可以和三次根号约去。

求一个数a的立方根的运算叫做开立方。

复数范围内，任何数有且只有三个立方根，它们均匀分布在以原点为圆心，算术根为半径的圆周上，三个立方根对应的点构成正三角形。立方根的性质 :⑴复数范围内，任何不是0的数都有3个立方根.⑵0的立方根是0。

五、1的立方根是多少

1的立方根是1,1的平方根也是1,1的4次方根也是1,同理1的N次方根同样是1