一、去心邻域什么意思？
去心邻域即在a的邻域中去掉a的数的集合，应用于高等数学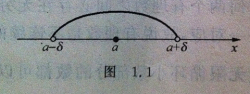
在拓扑学中，设A是拓扑空间(X,τ)的一个子集，点x∈A。如果存在集合U，满足 U 是开集，即 U∈τ；点x∈U；U 是A的子集，则称点 x 是 A 的一个内点，并称 A 是点 x 的一个邻域。
只考虑点a邻近的点，不考虑点a，即考虑点集{x|a-δ ，即 。 扩展资料： 高等数学中，我们经常会用到一种特殊的开区间 ，称这个开区间为点a的邻域（neighbourhood），记为 ，即 ，并称点a为邻域的中心，δ为邻域的半径 。通常δ是较小的实数，所以，a的δ邻域表示的是a的邻近的点 。以a为中心的任何开区间都称为点a的邻域，记作U(a)。设δ是任一正数，则开区间(a－δ，a+δ)就是点a的一个邻域，这个邻域称为点a的δ邻域。 参考资料来源：百度百科-去心邻域 去心邻域的理解即在a的邻域中去掉a的数的集合，应用于高等数学。在拓扑学中，设A是拓扑空间(X,τ)的一个子集，点x∈A。如果存在集合U，满足U是开集，即U∈τ；点x∈U；U是A的子集，则称点x是A的一个内点，并称A是点x的一个邻域。 高等数学中，我们经常会用到一种特殊的开区间，称这个开区间为点a的邻域（neighbourhood），记为，即，并称点a为邻域的中心，δ为邻域的半径。通常δ是较小的实数，所以，a的δ邻域表示的是a的邻近的点，如下图所示。若非空集合X的子集A是A内所有元素的邻域，则A为开集。 邻域是一个特殊的区间，以点a为中心点任何开区间称为点a的邻域，记作U(a)。 点a的δ邻域：设δ是一个正数，则开区间（a-δ，a+δ）称为点a的δ邻域，点a称为这个邻域的中心，δ称为这个邻域的半径。二、去心邻域怎么理解?
