一、同位角,内错角,同旁内角分别是怎样定义的
同位角,即位置相同,两个角都在第三条直线的同旁,同在被截两条直线的上方或下方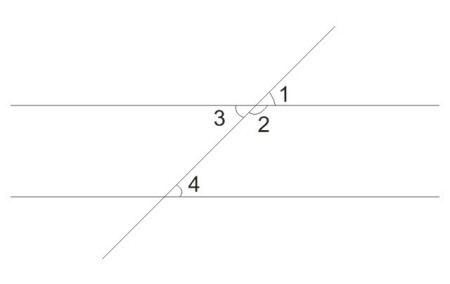
内错角,“内”指在被截两条直线之间;“错”即交错,在第三条直线的两侧。(一个角在第三直线 左侧,另一角在第三直线右侧)
同旁内角,“同旁”指在第三条直线的同侧;“内”指在被截两条直线之间。
两条直线被第三条直线所截所形成的八个角中,有四对同位角,两对内错角,两对同旁内角。
二、同位角,内错角,同旁内角的概念分别是什么?
1.两条直线a,b被第三条直线c所截(或说a,b相交c),在截线c的同旁,被截两直线a,b的同一侧的角,我们把这种两个角称为同位角。
图中的∠1与∠5是一组同位角。
2.两条平行直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫做内错角。
图中的∠4与∠6是一组内错角。
3.两条直线被第三条直线所截,在截线同旁,且在被截线之内的两角,叫做同旁内角。同旁内角,“同旁”指在第三条直线的同侧;“内”指在被截 两条直线之间。
图中的∠3与∠6是一组同旁内角。
三、同位角,内错角,同旁内角是什么概念(请作图分析)
1、两条直线被第三条直线所截,在截线的同旁,被截两直线的同一方,我们把这种位置关系的角称为同位角。互为同位角的有:∠1与∠5,∠2与∠6,∠4与∠7,∠4与∠8。
2、两条直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫做内错角。互为内错角的有:∠3与∠5,∠4与∠6。
3、两条直线被第三条直线所截,在两条直线之间,并在第三条直线同旁的两个角称为同旁内角。互为同旁内角的有:∠3与∠6,∠4与∠5。
扩展资料:
其他角的概念:
1、余角和补角:两角之和为90°则两角互为余角,两角之和为180°则两角互为补角。等角的余角相等,等角的补角相等。
2、对顶角:两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线,这样的两个角叫做互为对顶角。两条直线相交,构成两对对顶角。互为对顶角的两个角相等。
3、邻补角:两个角有一条公共边,它们的另一条边互为反向延长线,具有这种关系的两个角,互为邻补角。
四、“同位角,内错角,同旁内角”是什么概念?
同位角:两条直线a,b被第三条直线c所截(或说a,b相交c),在截线c的同旁,被截两直线a,b的同一侧的角,我们把这样的两个角称为同位角。
内错角:两条直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫做内错角(alternate angle)。
同旁内角:两条直线被第三条直线所截,在截线同旁,且在被截线之内的两角,叫做同旁内角。同旁内角,“同旁”指在第三条直线的同侧;“内”指在被截两条直线之间。两直线平行,同旁内角互补。同旁内角互补,两直线平行。
在几何学中,角是由两条有公共端点的射线组成的几何对象。这两条射线叫做角的边,它们的公共端点叫做角的顶点。一般的角会假设在欧几里得平面上,但在欧几里得几何中也可以定义角。角在几何学和三角学中有着广泛的应用。
几何之父欧几里得曾定义角为在平面中两条不平行的直线的相对斜度。普罗克鲁斯认为角可能是一种特质、一种可量化的量、或是一种关系。欧德谟认为角是相对一直线的偏差,安提阿的卡布斯认为角是二条相交直线之间的空间。欧几里得认为角是一种关系,不过他对直角、锐角或钝角的定义都是量化的的。
五、什么是同位角,内错角,同旁内角互补
同位角:在截线同旁,被截线相同的一侧的两角。
内错角:在截线两旁,被截线之内的两角
同旁内角:在截线同旁,被截线之内的两角两条平行直线与另一条直线相交,这三条线围起来的里面的两个角叫同旁内角;互补就是两个角加起来等于180度。