一、如何寻找间断点？
设一元实函数f（x）在点x0的某去心邻域内有定义.如果函数f(x)有下列情形之一：（1）在x=x0没有定义； （2）虽在x=x0有定义,但x→x0 limf(x)不存在； （3）虽在x=x0有定义,且x→x0 limf(x)存在,但x→x0 limf(x)≠f(x0),则函数f(x)在点x0为不连续,而点x0称为函数f(x)的间断点.
几种常见类型.可去间断点：函数在该点左极限、右极限存在且相等,但不等于该点函数值或函数在该点无定义.如函数y=（x^2-1)/(x-1)在点x=1处.（图一） 跳跃间断点：函数在该点左极限、右极限存在,但不相等.如函数y=|x|/x在点x=0处.（图二） 无穷间断点：函数在该点可以有定义,且左极限、右极限至少有一个为∞.如函数y=tanx在点x=π/2处.（图三） 振荡间断点：函数在该点可以有无定义,当自变量趋于该点时,函数值在两个常数间变动无限多次.如函数y=sin(1/x)在x=0处.（图四） 可去间断点和跳跃间断点称为第一类间断点,也叫有限型间断点.其它间断点称为第二类间断点.由上述对各种间断点的描述可知,函数f(x)在第一类间断点的左右极限都存在,而函数f(x)在第二类间断点的左右极限至少有一个不存在,这也是第一类间断点和第二类间断点的本质上的区别.
二、间断点的判断方法
判断方法首先找出函数没有意义的点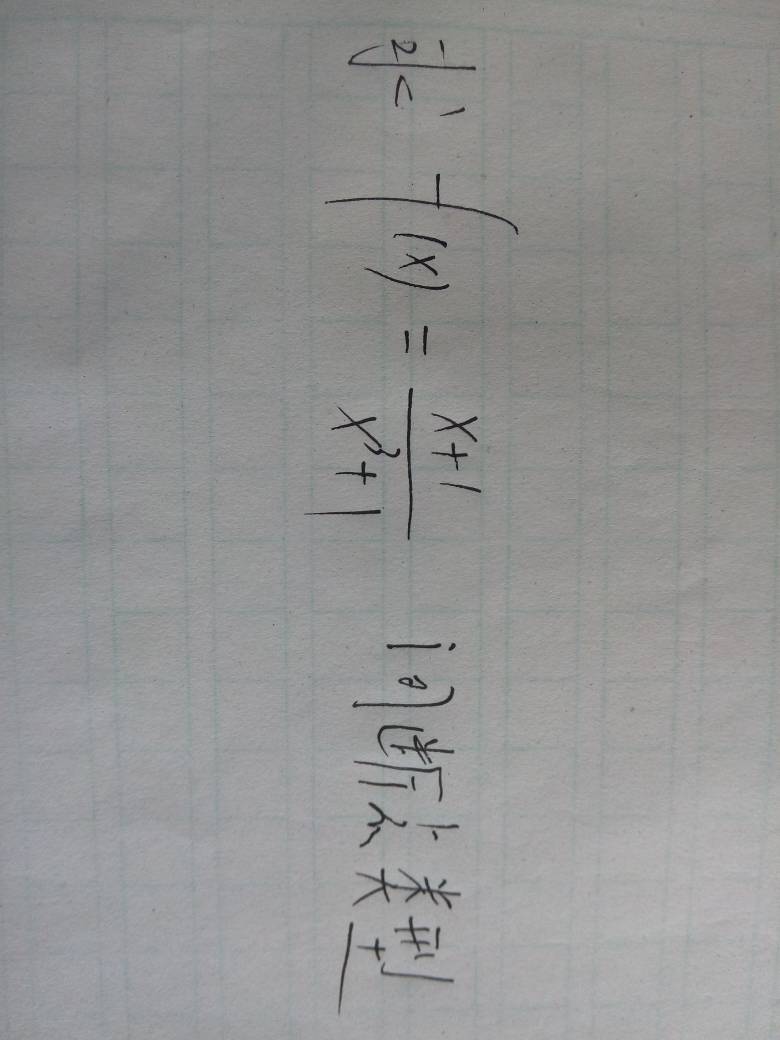
第一类间断点包括第一类可去间断点和第一类不可去间断点，如果该点左右极限都存在，则是第一类间断点，其中如果左右极限相等，则是第一类可去间断点，如果左右极限不相等，则是第一类不可去间断点，即第一类跳跃间断点。
如果函数f在点x连续，则称x是函数f的连续点；如果函数f在点x不连续，则称x是函数f的间断点。
间断点是指在非连续函数y=f(x)中某点处xo处有中断现象，那么，xo就称为函数的不连续点。间断点可以分为无穷间断点和非无穷间断点，在非无穷间断点中，还分可去间断点和跳跃间断点。左右极限存在且相等是可去间断点，左右极限存在且不相等才是跳跃间断点。
间断点的类型，有第一类间断点：其中包括可去间断点（左右极限相等此点无意义）、跳跃间断点（左右极限不相等）
第二类间断点：震动间断点（函数值在上下来回震动）、无限间断点（函数值）。以上就是关于间断点的相关内容，可以看看一看是否是这样
三、怎么求间断点
如果函数f(x)有下列情形之一：
（1）函数f(x)在点x0的左右极限都存在但不相等，即f(x0+)≠f(x0-)；
（2）函数f(x)在点x0的左右极限中至少有一个不存在；
（3）函数f(x)在点x0的左右极限都存在且相等，但不等于f(x0)或者f(x)在点x0无定义。
则函数f(x)在点x0为不连续，而点x0称为函数f(x)的间断点。
扩展资料：
间断点的分类：
1、可去间断点：函数在该点左极限、右极限存在且相等，但不等于该点函数值或函数在该点无定义。如函数y=（x^2-1)/(x-1)在点x=1处。
2、跳跃间断点：函数在该点左极限、右极限存在，但不相等。如函数y=|x|/x在点x=0处。
3、无穷间断点：函数在该点可以无定义，且左极限、右极限至少有一个不存在，且函数在该点极限为∞。如函数y=tanx在点x=π/2处。
4、振荡间断点：函数在该点可以无定义，当自变量趋于该点时，函数值在两个常数间变动无限多次。如函数y=sin(1/x)在x=0处。
可去间断点和跳跃间断点称为第一类间断点，也叫有限型间断点。其它间断点称为第二类间断点。
参考资料来源：百度百科-间断点
四、间断点一般怎么找
f(x)在点x0没有定义 ，只要是该点不在函数的定义域内就是间断点 。
函数间断点寻找的方法:无定义的点、就是间断点。
例：f(x)=x(x不等于1），x=1时f（x）=3。这里函数在1的极限为1不等于该点定义的值，所以间断 对于（3）就是判断左右极限是否相等并且等不等于该点定义的值。
可去间断点即左极限=右极限=有限值,与此点取值、有无定义均无关,可以通过重新定义让其连续的点。分母为0的“有限点”（不算x→∞）都有可能是可去间断点。
五、判断间断点的技巧
判断间断点的技巧：
1、第一类间断点：该点左右极限都存在，可分为：
（1）可去间断点：左右极限相等。
（2）跳跃间断点：左右极限不相等。
2、第二类间断点：左右极限中有一个不存在，可分为：
（1）无穷间断点：在间断点的极限为无穷大。
（2）震荡间断点：在间断点的极限不稳定存在。
间断点是指：在非连续函数y=f(x)中某点处xo处有中断现象，那么，xo就称为函数的不连续点。
设函数f（x）在点x0的某去心邻域内有定义。如果函数f(x)有下列情形之一：
（1）在点x0的左右极限都存在但不相等，即f(x0+)≠f(x0-)；
（2）在点x0的左右极限至少有一个不存在；
（3）在点x0的左右极限存在且相等，但不等于f(x0)或者f(x)在点x0无定义。
则函数f(x)在点x0为不连续，点x0称为函数f(x)的间断点。
