一、极限函数lim重要公式16个
极限函数lim重要公式16个如下:
1、e^x-1~x(x→0)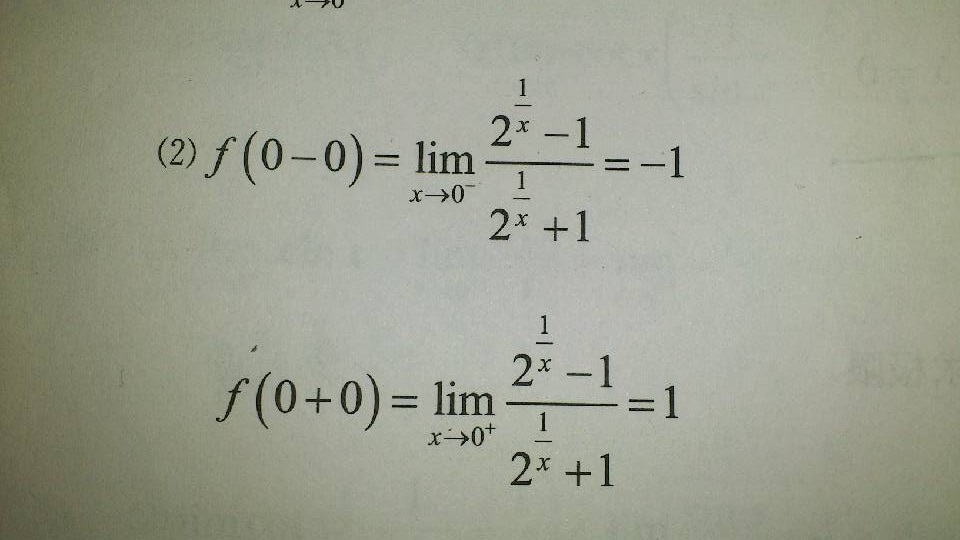
2、e^(x^2)-1~x^2(x→0)。
3、1-cosx~1/2x^2(x→0)。
4、1-cos(x^2)~1/2x^4(x→0)。
5、sinx~x(x→0)。
6、tanx~x(x→0)。
7、arcsinx~x(x→0)。
8、arctanx~x(x→0)。
9、1-cosx~1/2x^2(x→0)。
10、a^x-1~xlna(x→0)。
11、e^x-1~x(x→0)。
12、ln(1+x)~x(x→0)。
13、(1+Bx)^a-1~aBx(x→0)。
14、[(1+x)^1/n]-1~1/nx(x→0)。
15、loga(1+x)~x/lna(x→0)。
16、limα→0(1+α)1α=e。
“极限”是数学中的分支微积分的基础概念,广义的“极限”是指“无限靠近而永远不能到达”的意思。微积分中的极限是基础概念,它指的是变量在一定的变化过程中,从总的来说逐渐稳定的这样一种变化趋势以及所趋向的值(极限值)。
二、lim极限函数公式总结是什么?
求极限lim的常用公式有:
1、lim(f(x)+g(x))=limf(x)+limg(x);
2、lim(f(x)-g(x))=limf(x)-limg(x);
3、lim(f(x)×g(x))=limf(x)×limg(x);
4、lim(f(x)/g(x))=limf(x)/limg(x)limg(x)不等于0;
5、lim(f(x))^n=(limf(x))^n。
极限的求法有很多种:
1、连续初等函数,在定义域范围内求极限,可以将该点直接代入得极限值,因为连续函数的极限值就等于在该点的函数值。
2、利用恒等变形消去零因子(针对于0/0型)。
3、利用无穷大与无穷小的关系求极限。
4、利用无穷小的性质求极限。
5、利用等价无穷小替换求极限,可以将原式化简计算。
三、极限中有哪些重要极限公式?
主要是两个重要极限。
供参考,请笑纳。