一、等额本金和等额本息哪个更划算
两者各有利弊,可根据个人情况选择。
平均资本中的月还款额不同,呈现逐月递减的状态。 等额本息就是相同的月还款额。 本质上是本金比例逐月增加,利息比例逐月减少,每月还款次数不变。
两者的区别:
1.月还款额不同:平均资本中的月还款额是递减的。 平均资本的偿还将固定为每月相同的本金金额,而利息金额将随每月减少。 等额本息就是每个月还相同的金额,利息在提前还款中占很大比例。
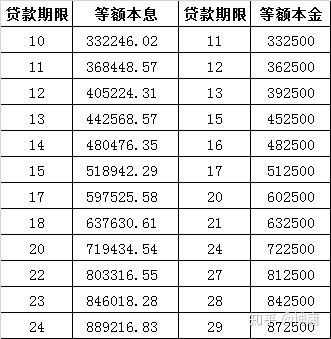
2.产生的利息不一样:等额本金还款法的总利息小于等额本金还款法的总利息。 比如贷款50万,贷款期限一年,贷款年利率4.35%。 等额本金还款总利息为2356.25元,等额本金还款总利息为2371.88元。
3.适合不同人群:一般资本适合前期收入较高,后期收入较低的人群。 关键老肢等额本息适合月收入固定的人
4.利弊不同:一般资金的好处是可以节省更多的利息,有利于提前还款,缺点是提前还款压力大。 等额本息的好处是每月还款压力小,坏处是需要多付利息,不利于提前还款。
二、买房贷款,等额本息和等额本金哪个更划算?
等额本息好。
按揭贷款一般采用等额本息的还款方式,大部分银行也默认这种还款方式。其中只有少数采用平均资本的还款方式,一般需要客户主动申请,所以银行会采用平均资本作为抵押贷款的还款方式。
银行之所以这么做,是因为如果房贷采用等额本息还款方式,客户需要支付更多利息,银行可以收取更多利息,有利于收益;还有,如果采用平均资本还款方式,客户前期还款压力较大,所以对客户的信用条件要求较高,需要客户有一定的经济基础和稳定的经济来源,否则逾期还款的可能性较大。
如果客户经济条件较差,在房贷还款初期不适合过多的资金投入,选择等额本息还款方式比较好。如果客户不想付太多利息,可以在有钱的时候提前还款,这样可以减少利息,降低借贷成本。
等额本息还款的计算公式是什么:
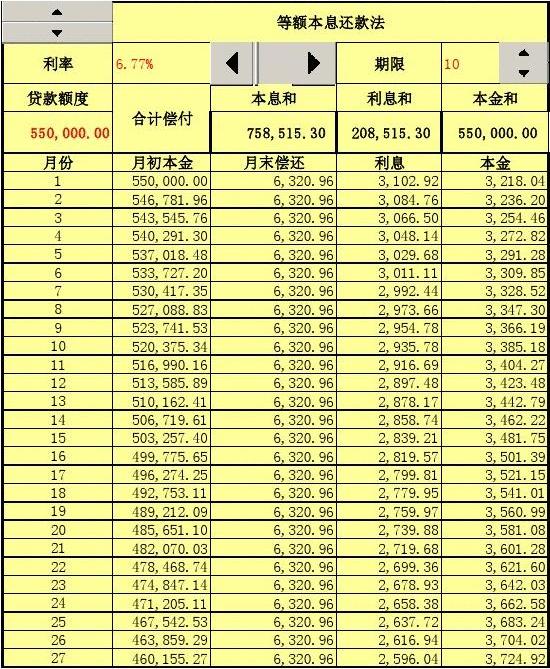
一般个人购房按揭贷款的期限都在一年以上,所以还款方式之一是等额本息还款法,即从使用贷款的第二个月起,每月平均等额偿还贷款本息。计算公式如下:
[贷款本金×月利率×(1+月利率)还款月数];[(1+月利率)还款月数-1]
下面举例说明等额本息还款方式。
假设借款人从银行获得个人住房贷款20万元,贷款期限20年,贷款年利率4.2%,每月还本付息。根据上述公式,每月应付本息之和为1233.14元。
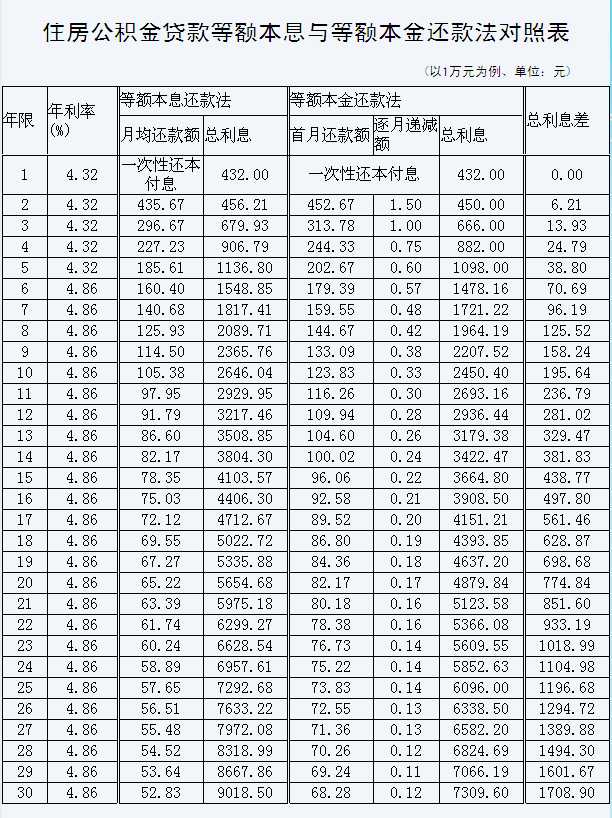
等额本息和平均资本有什么区别:
等额本金还款就是每月等额偿还本金,然后根据剩余本金计算利息。所以初期由于本金多,会多付利息,这样初期还款金额会多,后续每个月都会减少。这种方式的好处是,更适合还款能力强的家庭,减少初期因大额还款而产生的利息支出。
等额本息还款是在还款期内,每月偿还相同金额的贷款(包括本金和利息)。由于每月还款额是固定的,可以有计划地控制家庭收入的支出,也便于每个家庭根据自己的收入确定自己的还款能力。
三、30年房贷等额本息和等额本金哪个划算
如果利率、额度等都相同,那么是等额本金更划算,等额本金还款的计算方式利息要比等额本息更少。不过等额本金的初期还款比较多,对于贷款人的收入要求较高,不一定适合所有人,即使能够负担,压力也很多,建议还是结合自己的情况选择。
拓展资料:等额本金和等额本息有何区别
一、利息的算法不同
1、等额本息法的算法
每月还本付息金额=[本金*月利率*(1+月利率)*贷款月数]/[(1+月利率)*还款月数-1]
每月利息=剩余本金*贷款月利率
还款总利息=贷款额*贷款月数*月利率*(1+月利率)*贷款月数/[(1+月利率)*还款月数-1]-贷款额
还款总额=还款月数*贷款额*月利率*(1+月利率)*贷款月数/[(1+月利率)*还款月数-1]
注意:在等额本息法中,银行是先收利息,后收本金的,也因此每月的利息随着本金的减少而减少,但每个月所交的总金额是不会变的。
2、等额本金法的算法
每月还本付息金额=(本金/还款月数)+(本金-累计已还本金)×月利率
每月本金=总本金/还款月数
每月利息=(本金-累计已还本金)*月利率
还款总利息=(还款月数+1)*贷款额*月利率/2
还款总额=(还款月数+1)*贷款额*月利率/2+贷款额
注意:在等额本金法中,人们缴纳的本金是不变的,但每月所交的利息是随本金减少而减少,所以每个月的还款总额是递减的。
由此可以看出,本金相同的情况下,等额本息所要付的利息比等额本金支出的要多,而且这个差额是随着贷款时间成正比的。
二、适合的人群不同
1、等额本息每月缴纳的还款数额相同,比较适合每月有固定收入的家庭,尤其是对与青年人,随着自己在职经历的增加,有可能会升职,这就意味着收入的提高,从而缓解贷款压力,提高生活质量。但若是选择了等额本金的话,前期的资金压力就非常大了。
2、等额本金法前期的付款额度较大,而后逐月递减,所以比较适合有一定存款的用户或者是工作能力强未来收入预期良好的用户,也只有有一定资金实力的人比较容易负担得起等额本金的前额付款。