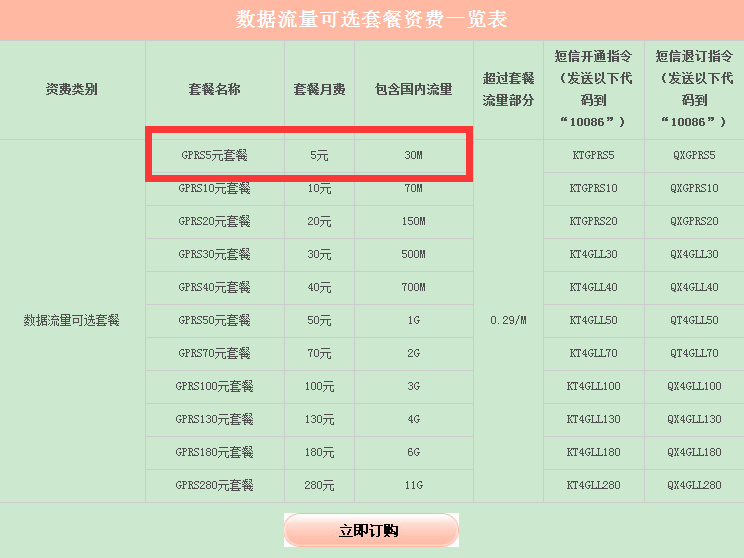
一、如何理解哈密顿
这是与牛顿力学等价的另一种描述经典力学的理论,也就是哈密顿力学,其中的重要量
不知道题主是什么程度,我按照我自己的理解来解释了。
哈密顿力学是经典力学的表现形式之一,用广义坐标和广义动量描述运动,用正则方程描述坐标和动量的演化,用哈密顿量来写正则方程。所以,构建一个物理系统,就是构建它的哈密顿量。作为比较,对于牛顿力学就是构建力的表达式,拉格朗日力学就是构建拉氏量。
二、哈密顿量是什么意思?
哈密顿量是系统的能量算符,所谓哈密顿量的对角化就是解一个本征值问题(在线性代数中就是特征值和特征向量)。对角化哈密顿量的过程就是一个找能量本征值的过程(找到这个系统可能存在的能量)。或者是一个去耦合的过程(比如说两个弹簧振子振动时存在耦合,可以写成一个哈密顿量的形势,对角化后,找到了弹簧真子的简振模,就去耦合了) 对角化的物理含义就是找到一个能量系统中的可能能量(一般来说这些能量都是分立的,这就是量子力学的精髓之一) 在势场V(x)中的粒子,其经典哈密顿量H=T+V的算符表示成 Hamilton算符=动能算符+势能,势能是与位置X相关的量,没有相应的算符表示,而动能算符表示为 (动量算符的平方/两倍的质量)。 动量算符的表达形式在计算自由粒子动量平均值的过程中通过自由粒子在坐标和动量表象下的波函数变换求出。具体的公式推导可以去看量子力学。 薛定谔方程的表达形式就是哈密顿量本征函数的形式