一、什么叫方程两边分别对x求导数
方程两边分别求导的前提是：方程表示的是一个恒等式，而且可微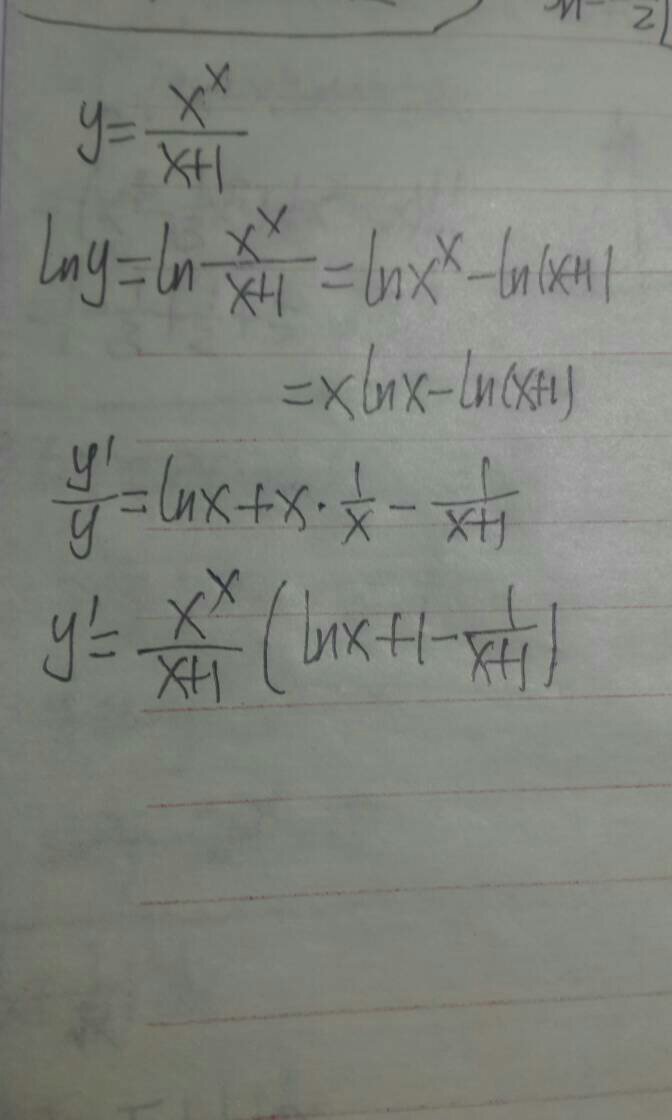
通常函数式就是一个恒等式，有一个X值就对应一个Y值。方程两边对X求导就是两边对自变量X求导，如果碰到X的函数必须一直求到X为止。
二、对X求导是什么意思
求导是数学计算中的一个计算方法，它的定义就是，当自变量的增量趋于零时，因变量的增量与自变量的增量之商的极限。在一个函数存在导数时，称这个函数可导或者可微分。可导的函数一定连续。不连续的函数一定不可导。
对x的求导求x 的可微分。只对这个数里面的x求导剩下的乘以对x求导的结果。
对x求导等于1。
具体简单函数导数如下：
扩展资料：
导数的计算
计算已知函数的导函数可以按照导数的定义运用变化比值的极限来计算。在实际计算中，大部分常见的解析函数都可以看作是一些简单的函数的和、差、积、商或相互复合的结果。
只要知道了这些简单函数的导函数，那么根据导数的求导法则，就可以推算出较为复杂的函数的导函数。
导数的求导法则
由基本函数的和、差、积、商或相互复合构成的函数的导函数则可以通过函数的求导法则来推导。基本的求导法则如下：
1、求导的线性：对函数的线性组合求导，等于先对其中每个部分求导后再取线性组合（即①式）。
2、两个函数的乘积的导函数：一导乘二+一乘二导（即②式）。
3、两个函数的商的导函数也是一个分式：（子导乘母-子乘母导）除以母平方（即③式）。
4、如果有复合函数，则用链式法则求导。
参考资料：百度百科-导数
三、怎么叫做“方程两边对x求导”？
先知道隐函数及复合函数的求导概念。对方程的每一项，无论带x的还是带y的项都进行求导，对x的项进行求导时就跟正常的求导一样，对含有y的项进行求导时，要将y看成是x的函数y(x),所以对y的求导需要复合函数求导法。
比如x^2+y^2=xy
x^2的求导为2x
y^2的求导为2yy'
xy的求导为y+xy'
故有 2x+2yy'=y+xy'
这样就可以解出y'=(y-2x)/(2y-x)了。
四、高数 什么叫两边对x求导啊？
就是把y看作f(x)，隐函数求导里的。
高等数学（也称为微积分,它是几门课程的总称）是理、工科院校一门重要的基础学科。作为一门科学，高等数学有其固有的特点，这就是高度的抽象性、严密的逻辑性和广泛的应用性。抽象性是数学最基本、最显著的特点--有了高度抽象和统一，我们才能深入地揭示其本质规律，才能使之得到更广泛的应用。
严密的逻辑性是指在数学理论的归纳和整理中，无论是概念和表述，还是判断和推理，都要运用逻辑的规则，遵循思维的规律。所以说，数学也是一种思想方法，学习数学的过程就是思维训练的过程。
人类社会的进步，与数学这门科学的广泛应用是分不开的。尤其是到了现代，电子计算机的出现和普及使得数学的应用领域更加拓宽，现代数学正成为科技发展的强大动力，同时也广泛和深入地渗透到了社会科学领域。
