一、x的lnx的导数怎么求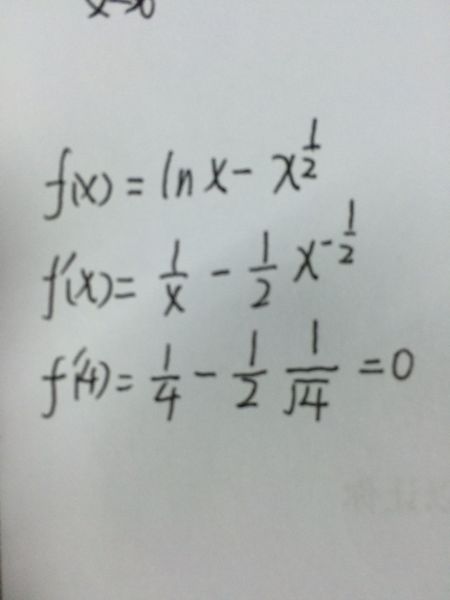
(x^lnx)'=(e^((lnx)^2))'
用复合函数求导:
原式
=e^((lnx)^2)*2lnx*1/x
=2*x^(lnx-1)*lnx
扩展资料:
当自变量的增量趋于零时,因变量的增量与自变量的增量之商的极限。在一个函数存在导数时,称这个函数可导或者可微分。可导的函数一定连续。不连续的函数一定不可导。
如果函数的导函数在某一区间内恒大于零(或恒小于零),那么函数在这一区间内单调递增(或单调递减),这种区间也称为函数的单调区间。导函数等于零的点称为函数的驻点,在这类点上函数可能会取得极大值或极小值(即极值可疑点)。
二、xlnx导数过程
如题所示:
当自变量的增量趋于零时,因变量的增量与自变量的增量之商的极限。在一个函数存在导数时,称这个函数可导或者可微分。可导的函数一定连续。不连续的函数一定不可导。
函数 被称为幂指函数,在经济活动中会大量涉及此类函数,注意到它很特别。既不是指数函数又不是幂函数,它的幂底和指数上都有自变量x,所以不能用初等函数的微分法处理了。这里介绍一个专门解决此类函数的方法,对数求导法。
对于 两边取对数(当然取以为e底的自然对数计算更方便)。由对数的运算性质。
扩展资料:
不是所有的函数都可以求导;
可导的函数一定连续,但连续的函数不一定可导(如y=|x|在y=0处不可导)。
函数y=f(x)在x0点的导数f'(x0)的几何意义:表示函数曲线在点P0(x0,f(x0))处的切线的斜率(导数的几何意义是该函数曲线在这一点上的切线斜率)。
由基本函数的和、差、积、商或相互复合构成的函数的导函数则可以通过函数的求导法则来推导。基本的求导法则如下:
1、求导的线性:对函数的线性组合求导,等于先对其中每个部分求导后再取线性组合(即①式)。
2、两个函数的乘积的导函数:一导乘二+一乘二导(即②式)。
3、两个函数的商的导函数也是一个分式:(子导乘母-子乘母导)除以母平方(即③式)。
4、如果有复合函数,则用链式法则求导。
参考资料:百度百科——求导
三、xlnx的导数
∵y=xlnx
∴y′=lnx+x(1/x)
=1+lnx,
故答案为:1+lnx 扩展资料 函数y=xLnx的N阶导数
Y=XLnX
Y’=LnX+1 Y’’=1/X
Y(n)=(Y’’)(n-2)
=(1/X)(n-2)
=(-1)n/Xn-1
Y(n) = LnX+1 (n=1)
= (-1)n/Xn-1 (n>1)
注意:上面有些是上标,带括号的.表示n阶导数,不带的表示幂指数
四、x的lnx次方的导数怎么求
y=x^lnx
对数求导法:
两边同时取对数得:
lny=(lnx)^2
求导得:
y'/y=2lnx/x
y'=2x^(-1)(lnx)x^lnx
y'=2(lnx)x^(lnx-1)
不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在,则称其在这一点可导,否则称为不可导。然而,可导的函数一定连续;不连续的函数一定不可导。
扩展资料:
如果函数y=f(x)在开区间内每一点都可导,就称函数f(x)在区间内可导。这时函数y=f(x)对于区间内的每一个确定的x值,都对应着一个确定的导数值,这就构成一个新的函数,称这个函数为原来函数y=f(x)的导函数,记作y'、f'(x)、dy/dx或df(x)/dx。
基本函数的和、差、积、商或相互复合构成的函数的导函数则可以通过函数的求导法则来推导。基本的求导法则如下:
1、求导的线性:对函数的线性组合求导,等于先对其中每个部分求导后再取线性组合(即①式)。
2、两个函数的乘积的导函数:一导乘二+一乘二导(即②式)。
3、两个函数的商的导函数也是一个分式:(子导乘母-子乘母导)除以母平方(即③式)。
4、如果有复合函数,则用链式法则求导。
五、xlnx的导函数是什么
利用乘积的导数公式,得
(xlnx)'=lnx+x * 1/x
=lnx+1 。