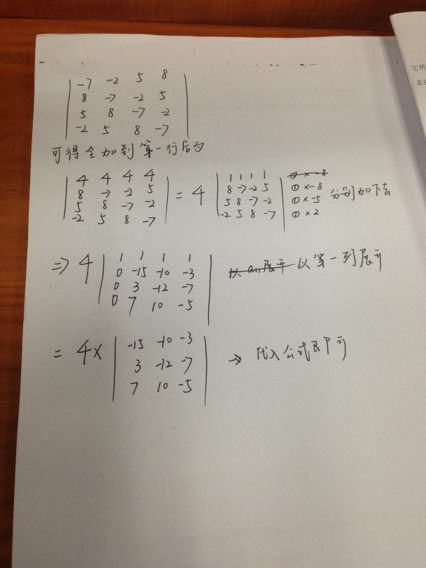可逆矩阵的逆矩阵是唯一的吗?
(A^-1)(A+B)(B^-1)=B^-1+A^-1
由于可逆阵的逆阵可逆,可逆阵的乘积可逆,由上式知:A^-1
+B^-1可逆.再由性质:(AB)^-1=(B^-1)(A^-1)由(**)式,两端取逆
得:(A^-1+B^-1)^-1==[(B^-1)]^-1}[(A+B)^-1][(A^-1)^-1]=(B)[(A+B)^-1](A)
可逆矩阵的性质:
1、可逆矩阵一定是方阵。
2、如果矩阵A是可逆的,其逆矩阵是唯一的。
3、A的逆矩阵的逆矩阵还是A。记作(A-1)-1=A。
4、可逆矩阵A的转置矩阵AT也可逆,并且(AT)-1=(A-1)T (转置的逆等于逆的转置)。
5、若矩阵A可逆,则矩阵A满足消去律。即AB=O(或BA=O),则B=O,AB=AC(或BA=CA),则B=C。
抽象矩阵的逆矩阵唯一吗
是唯一的哈。如果是具体的矩阵,它的逆矩阵的结果肯定唯一。
如果这个矩阵是一个字母,可能得到的矩阵的逆的书写形式结果不唯一,其实它们都是相等的
一个矩阵的可逆矩阵是唯一的吗?
是唯一的。
如果A
是可逆矩阵,那么当B,C都是A的逆时,有
AB=BA=E=AC=CA
,
B=BE=B(AC)=
(BA)C=EC=C
所以是唯一的。
n阶矩阵A的逆矩阵唯一吗?
n阶矩阵A可逆的充要条件:
1、|A|不等于0。
2、r(A)=n。
3、A的列(行)向量组线性无关。
4、A的特征值中没有0。
5、A可以分解为若干初等矩阵的乘积。
矩阵A为n阶方阵,若存在n阶矩阵B,使得矩阵A、B的乘积为单位阵,则称A为可逆阵,B为A的逆矩阵。若方阵的逆阵存在,则称为可逆矩阵或非奇异矩阵,且其逆矩阵唯一。
n阶矩阵A可逆介绍:
数aij位于矩阵A的第i行第j列,称为矩阵A的(i,j)元,以数 aij为(i,j)元的矩阵可记为(aij)或(aij)m × n,m×n矩阵A也记作Amn。
元素是实数的矩阵称为实矩阵,元素是复数的矩阵称为复矩阵。而行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵。
矩阵分解是将一个矩阵分解为比较简单的或具有某种特性的若干矩阵的和或乘积 ,矩阵的分解法一般有三角分解、谱分解、奇异值分解、满秩分解等。
三阶矩阵逆矩阵唯一吗
您好,感谢您提出这个问题。三阶矩阵逆矩阵不一定是唯一的,它可能有多个逆矩阵。一般来说,如果一个矩阵的行列式不等于零,那么它就有唯一的逆矩阵;如果行列式等于零,那么它就可能有多个逆矩阵,或者没有逆矩阵。因此,三阶矩阵逆矩阵不一定是唯一的,它可能有多个逆矩阵,也可能没有逆矩阵。