一、拉普拉斯分块矩阵公式是什么？
设两方阵A(n*n)，B(m*m)在副对角线上，通过矩阵的列变换将A，B移到主对角线上，然后用拉普拉斯展开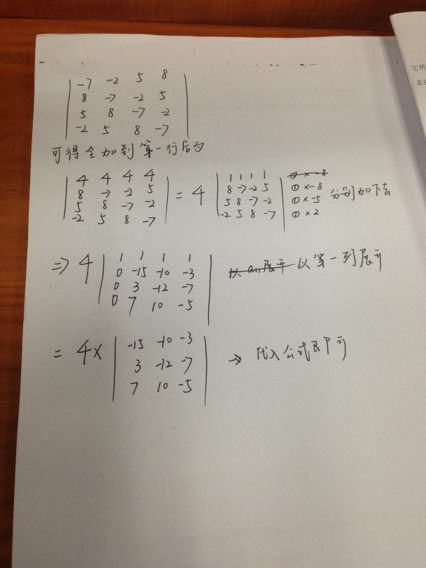
A的第一列列变换m次，A的第二列列变换也是m次，依此类推，A的第n列的列变换也是m次，可以得知列变换共进行了m*n次，列变换完成后，B已经移到主对角线上了，所以要乘(-1)^(m*n)。
设两方阵A(n*n)，B(m*m)在副对角线上，通过矩阵的列变换将A，B移到主对角线上，然后用拉普拉斯展开。A的第一列列变换m次，A的第二列列变换也是m次，依此类推，A的第n列的列变换也是m次，可以得知列变换共进行了m*n次，列变换完成后，B已经移到主对角线上了，所以要乘(-1)^(m*n)。
对矩阵进行适当分块，可使高阶矩阵的运算可以转化为低阶矩阵的运算，同时也使原矩阵的结构显得简单而清晰，从而能够大大简化运算步骤，或给矩阵的理论推导带来方便。
初等代数从最简单的一元一次方程开始，初等代数一方面进而讨论二元及三元的`一次方程组，另一方面研究二次以上及可以转化为二次的方程组。沿着这两个方向继续发展，代数在讨论任意多个未知数的一次方程组，也叫线性方程组的同时还研究次数更高的一元方程组。
发展到这个阶段，就叫做高等代数。高等代数是代数学发展到高级阶段的总称，它包括许多分支。现在大学里开设的高等代数，一般包括两部分：线性代数、多项式代数。
二、分块矩阵常用公式
计算公式如下：
1.加法
设，，用同样的方法对A，B进行分块，即，为同型矩阵，则。
2.数乘
设，k是任意数，定义分块矩阵与k的数乘为。
3.乘法
设A是阶矩阵，B是阶矩阵，即A的列数=B的行数，分块，，即A的列分块法=B的行分块法。
请点击输入图片描述
则A与B的乘积是阶分块矩阵，
其中，。
转置
设矩阵是阶分块矩阵，，则。
