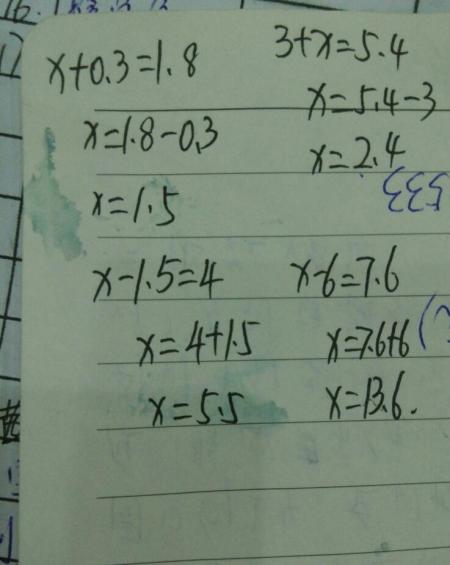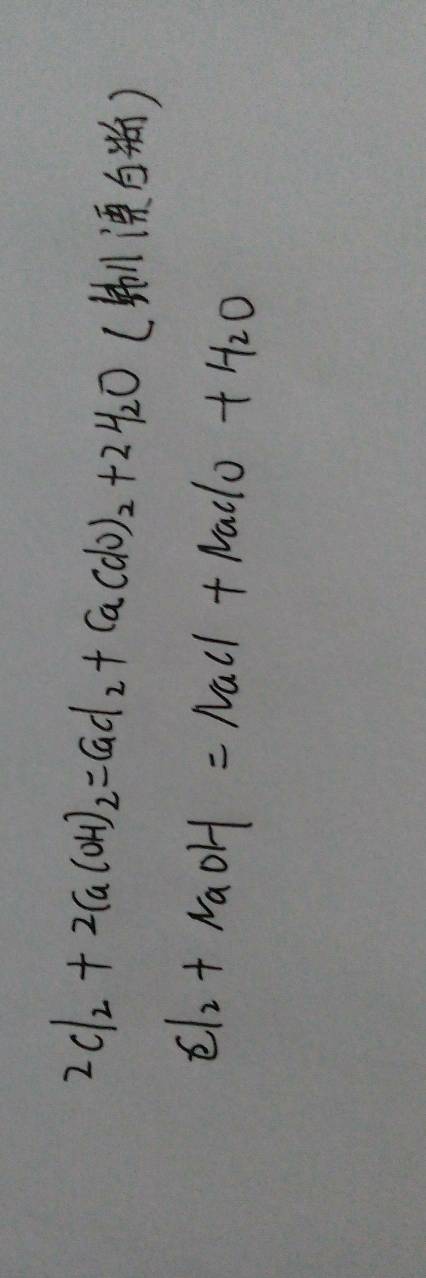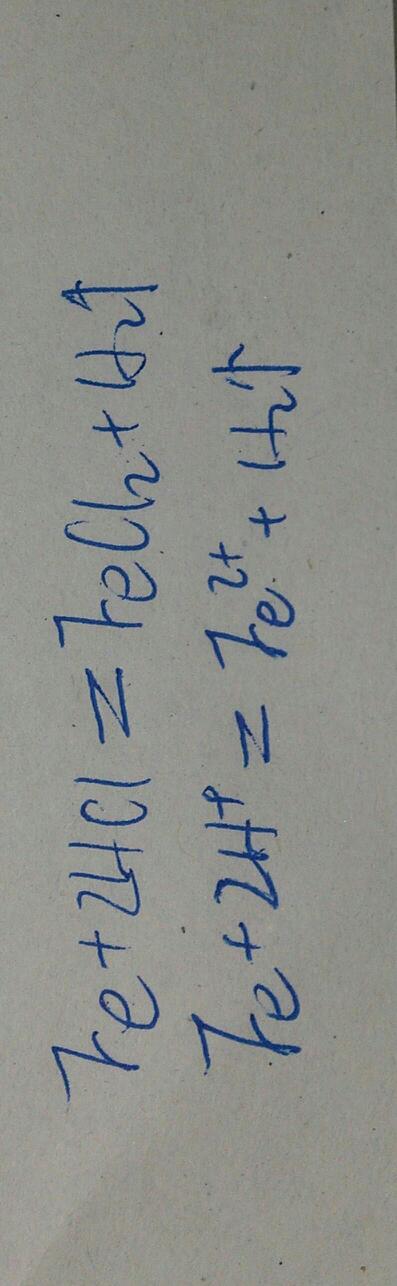双曲线准线的方程
双曲线有两条准线L1(左准线),L2(右准线),准线与双曲线的位置关系如右图所示
以原点为中心的双曲线 的准线的方程就是:x=±a²/c;
以原点为中心的双曲线 的准线的方程就是:y=±a²/c;
其中a是实半轴长,b是虚半轴长,c是半焦距。( )
例如,存在以原点为中心的双曲线 按照以上计算公式,则其准线方程为:
L1的方程: ;L2的方程: 。
双曲线的准线是什么?怎么得来的?谢谢!
平面内到一个定点与一条定直线的距离之比是一个大于1的常数的动点的轨迹是双曲线,这个常数即该双曲线的离心率,定点是双曲线的焦点,定直线是双曲线的准线。
计算公式(由来):双曲线上任意一点P与双曲线焦点的连线段,叫做双曲线的焦半径。设双曲线的焦点在x轴上。
设F1,F2为双曲线的左右焦点,x为P的横坐标,则P在左支上时:PF1=-(a+ex)PF2=-(ex-a)。P在右支上时:PF1=a+ex, PF2=ex-a.
扩展资料:
双曲线准线相关规律:
1、在标准方程中令x=0,得y²=-b²,该方程无实根,为便于作图,在y轴上画出B1(0,b)和B2(0,-b),以B1B2为虚轴。
2、双曲线有两个焦点,两条准线。(注意:尽管定义2中只提到了一个焦点和一条准线,但是给定同侧的一个焦点,一条准线以及离心率可以根据定义2同时得到双曲线的两支,而两侧的焦点,准线和相同离心率得到的双曲线是相同的。)
3、双曲线在实际中的应用有通风塔,冷却塔,埃菲尔铁塔,广州塔等。
参考资料来源:百度百科-双曲线准线
双曲线准线公式
双曲线准线的定义:平面内到一个定点与一条定直线的距离之比是一个大于1的常数的动点的轨迹是双曲线,这个常数即该双曲线的离心率,定点是双曲线的焦点,定直线是双曲线的准线。
双曲线上任意一点P与双曲线焦点的连线段,叫做双曲线的焦半径。
设双曲线的焦点在x轴上。
设F1,F2为双曲线的左右焦点,x为P的横坐标,则
P在左支上时:PF1=-(a+ex)PF2=-(ex-a)。
P在右支上时:PF1=a+ex, PF2=ex-a.
扩展资料:
几何性质
准线到顶点的距离为Rn/e,准线到焦点的距离为P = Rn(1+e)/e = L0/e 。
当离心率e大于零时,则P为有限量,准线到焦点的距离为P = Rn(1+e)/e = L0/e 。
当离心率e等于零时,则P为无限大,P是非普适量。用无限远来定义圆锥曲线是不符合常理的。
教科书中定义局限性的原因是不了解准线的几何性质,当e等于零时则准线为无限远,准线是非普适量,是局限性的量。教科书中用准线来定义圆锥曲线不包含圆的原因。
参考资料来源:百度百科-双曲线准线
双曲线的准线方程怎么推出来的?
双曲线的标准方程是x^2/a^2-y^2/b^1=1
(焦点在x轴)
或y^2/a^2-x^2/b^2=1(焦点在y轴)
点到直线的距离是垂直距离,点到点的距离是直线距离
双曲线焦点所在实轴,垂直于准线
设x=t说明焦点在x轴上
也可以设y=t(焦点在y轴)
如果设成一次斜率不为0的函数的直线
椭圆方程的实轴将不在x轴或y轴上
椭圆方程将是一个复杂的二次曲线形式。
双曲线准线方程
双曲线的准线的方程是:y=士a2ic。
双曲线方程:(x^2/a^2)-(y^2/b^2)=1。准线方程为:x=±a^2/c。双曲线的准线的方程就是:y=±a2/c;其中a是实半轴长,b是虚半轴长,c是半焦距。双曲线上各点到焦点的距离比上到准线的距离为离心率e。
双曲线上任意一点P与双曲线焦点的连线段,叫做双曲线的焦半径。设双曲线的焦点在x轴上。
怎样求双曲线的准线方程及准线间的距离?
设:椭圆方程为x2/a2+y2/b2=1,焦点为F1(c,0),F2(-c,0)(c>0);设:A(x,y)为椭圆上一点。
则,AF1=√[(x-c)2+y2]设:准线为x=f;则,A到准线的距离L为│f-x│;设:AF1/L=e,则(x-c)2+y2=e2(f-x)2;化简得(1-e2)x2-2xc+c2+y2-e2f2+2e2fx=0;令2c=2e2f。
则f=c/e2;令该点为右顶点则(c/e2-a)e=a-c;当e=c/a时上式成立;故f=a2/c。
双曲线准线方程?
双曲线的准线的方程就是:y=±a²/c,其中a是实半轴长,b是虚半轴长,c是半焦距。
椭圆和双曲线的第二定义是:平面上到定点距离与到定直线间距离之比为常数的点的集合(定点不在定直线上,该常数为小于1的正数)(该定点为椭圆的焦点,该直线称为椭圆的准线)。
圆锥曲线上任意一点到一焦点的距离与其对应的准线(同在Y轴一侧的焦点与准线)对应的距离比为离心率。椭圆上任意一点到焦点距离与该点到相应准线距离的比等于离心率e。
扩展资料:
注意事项:
构成满足(与椭圆焦半径不同,椭圆焦半径要带符号计算,而双曲线不带符号)
等轴双曲线:双曲线称为等轴双曲线,其渐近线方程为离心率。
共轭双曲线:以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线,叫做已知双曲线的共轭双曲线.与互为共轭双曲线,具有共同的渐近线。
参考资料来源:百度百科-双曲线准线