一、三角形角度计算公式是什么？

三角形角度计算公式：

1、cosA=b^2+c^2-a^2/2bc或a^2=b^2+c^2-2bccosA

2、cosB=c^2+a^2-b^2/2ca或b^2=c^2+a^2-2accosB

3、cosC=a^2+b^2-c^2/2ab或c^2=a^2+b^2-2abcosC

三角形的分类

1、锐角三角形：三角形的三个内角都小于90度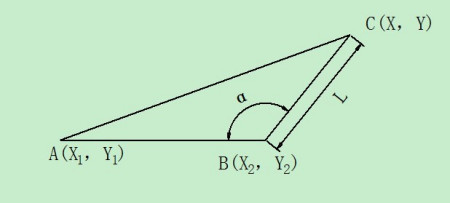

2、直角三角形：三角形的三个内角中一个角等于90度，可记作Rt△。

3、钝角三角形：三角形的三个内角中有一个角大于90度。

二、三角形的计算公式是什么

三角形的计算公式是什么

三角形的计算公式是什么，三角形是小学就会接触到的一个图形，之后在初中，高中以及之后的数学。三角形的计算，有关计算面积等等都会接触到，我们来一起看看关于三角形的计算公式是什么

三角形的计算公式是什么1

三角形正弦余弦公式大全

Sin(A-B)=SinA*CosB-SinB*CosA

Cos(A+B)=CosA*CosB-SinA*SinB

Tan(A+B)=(TanA+TanB)/(1-TanA*TanB)

sin(2α)=2sinα·cosα=2/(tanα+cotα)

cos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)

tan(2α)=2tanα/[1-tan^2(α)]

求三角形边长公式

三角形边长公式：1、根据余弦定理，有公式：a^2=b^2+c^2-2bc×cosA。2、根据正弦定理，有公式：a=b*sinA/sinB。3、根据勾股定理，有公式：a^2+b^2=c^2。

三角形边长的计算方法

对于任意一个三角形，已知两角一对边，可以根据正弦定理计算:a=b*sinA/sinB。正弦定理的公式为a/sinA = b/sinB =c/sinC，根据正弦定理的公式可以解三角形。

对于任意一个三角形，已知两条边与夹角，可以根据余弦定理求出第三条边，有公式：c^2=a^2+b^2-2abcosC、a^2=b^2+c^2-2bccosA、b^2=a^2+c^2-2accosB。余弦定理是描述三角形中三边长度与一个角的余弦值关系的数学定理，是勾股定理在一般三角形情形下的推广，勾股定理是余弦定理的特例。对于直角三角形，可以根据勾股定理求变成，有公式：a^2+b^2=c^2。

如何计算三角形的斜边

已知两个直角边，求第三边的方法有

已知一个锐角和两直角边，如图所示

已知直角三角形一锐角度数，求斜边的方法有正弦定理直接求出

还有通过正弦定理算出直角边，再用勾股定理求出

三角形的计算公式是什么2

已知三角形底a，高h，则

已知三角形三边a,b,c，则

（海伦公式）

S=sqrt[p(p-a)(p-b)(p-c)]

=sqrt[(1/16)(a+b+c)(a+b-c)(a+c-b)(b+c-a)]

=1/4sqrt[(a+b+c)(a+b-c)(a+c-b)(b+c-a)]

3.已知三角形两边a,b,这两边夹角C，则

即两夹边之积乘夹角正弦值的'一半。

设三角形三边分别为a、b、c，内切圆半径为r

则三角形面积

设三角形三边分别为a、b、c，外接圆半径为R

则三角形面积=abc/4R

S=2R·sinA·sinB·sinC

6.行列式形式

为三阶行列式，此三

在平面直角坐标系内

这里

选取最好按逆时针顺序从右上角开始取，因为这样取得出的结果一般都为正值，如果不按这个规则取，可能会得到负值，但不要紧，只要取绝对值就可以了，不会影响三角形面积的大小。该公式的证明可以借助“两夹边之积乘夹角的正弦值”的面积公式 [1] 。

海伦——秦九韶三角形中线面积公式:

S=√[(Ma+Mb+Mc)*(Mb+Mc-Ma)*(Mc+Ma-Mb)*(Ma+Mb-Mc)]/3

其中Ma,Mb,Mc为三角形的中线长.

8.根据三角函数求面积：

S= ab sinC=2R sinAsinBsinC= asinBsinC/2sinA

注:其中R为外切圆半径。

三、三角形的角度怎么算？

已知三角形边长，计算三角形的角度过程如下：

1、设三角形中角A所对应的边长是a，角B所对应的边长是b，角C所对应的边长是c。再利用公式：

①CosA=(c^2+b^2-a^2)/2bc

②CosB=(a^2+c^2-b^2)/2ac

③CosC=(a^2+b^2-c^2)/2ab

算出每一个角的余弦值，利用计算器上的反余弦函数功能就可以计算出各自的角度值。

2、如果三角形是钝角三角形，计算出的钝角的余弦值是负的，角度也就是负的，这时要加上180度才是钝角的角度。（注：a^2+b^2-c^2=0说明C的角度等于90度）

扩展资料：

一、已知三角形边，求角度，这种求法称之为“解三角形”。解三角形一般需要用到如下定理：

1、正弦定理

a/sinA=b/sinB=c/sinC=2R（2R在同一个三角形中是恒量，R是此三角形外接圆的半径）。

2、余弦定理

①a²=b²+c²-2bccosA

②b²=a²+c²-2accosB

③c²=a²+b²-2abcosC

二、三角形中已知某条件求未知量（如已知三边，求三个内角度数），一般有对应的公式：

1、以下情况利用正弦定理：

①已知条件：一边和两角（如a、B、C,或a、A、B）

一般解法：由A+B+C=180°，求角A，由正弦定理求出b与c，在有解时，有一解。

②已知条件：两边和其中一边的对角（如a、b、A）

一般解法：由正弦定理求出角B，由A+B+C=180°求出角C，再利用正弦定理求出C边，可有两解、一解或无解。（或利用余弦定理求出c边，再求出其余两角B、C）①若a>b，则A>B有唯一解；②若b>a，且b>a>bsinA有两解；③若a

2、以下情况利用余弦定理：

①已知条件：两边和夹角(如a、b、C）

一般解法：由余弦定理求第三边c，由正弦定理求出小边所对的角，再由A+B+C=180°求出另一角，在有解时有一解。

②已知条件：三边（如a、b、c）

一般解法：由余弦定理求出角A、B，再利用A+B+C=180°，求出角C在有解时只有一解。

参考资料：解三角形-百度百科

四、三角形角度计算公式是什么?

三角形角度计算公式有：

1、cosA=b^2+c^2-a^2/2bc或a^2=b^2+c^2-2bccosA。

2、cosB=c^2+a^2-b^2/2ca或b^2=c^2+a^2-2accosB。

3、cosC=a^2+b^2-c^2/2ab或c^2=a^2+b^2-2abcosC。

定理应用：

余弦定理是解三角形中的一个重要定理，可应用于以下三种需求：

当已知三角形的两边及其夹角，可由余弦定理得出已知角的对边。

当已知三角形的三边，可以由余弦定理得到三角形的三个内角。

当已知三角形的三边，可以由余弦定理得到三角形的面积。

三角形性质

1、在平面上三角形的内角和等于180°（内角和定理）。

2、在平面上三角形的外角和等于360°(外角和定理)。

3、在平面上三角形的外角等于与其不相邻的两个内角之和。

推论：三角形的一个外角大于任何一个和它不相邻的内角。