一、有限域证明是正确的,有什么意义
可以验证相关的推算是正确的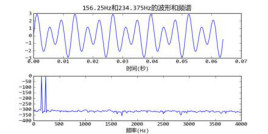
有限域亦称伽罗瓦域(galoisfield),是仅含有限个元素的域,它是伽罗瓦(Galois,E。)于18世纪30年代研究代数方程根式求解问题时引出的。
有限域的特征数必为某一素数p,因此它含的素域同构于Zp。若F是特征为p的有限域,则F中元素的个数为p_,n为某一正整数。元素个数相同的有限域是同构的。因此,通常用GF(p_)表示p_元的有限域。GF(p_)的乘法群是(p_-1)阶的循环群。
有限域在近代编码、计算机理论、组合数学等各方面有着广泛的应用。
二、什么是有限域
有限域:仅含有限多个元素的域。
定理:
一些小型的有限域
三、有限域的介绍
有限域是仅含有限多个元素的域。它首先由E.伽罗瓦所发现,因而又称为伽罗瓦域。它和有理数域、实数域比较,有着许多不同的性质。
四、有限域的概念
最简单的有限域是整数环Z 模一个素数p得到的余环Z/(p),由p个元素0,1,…,p-1组成,按模p相加和相乘。
J.H.M.韦德伯恩于1905年证明了“有限除环必是乘法交换的”。因此,有限除环就是现在所说的有限域。